泰森多边形的定义(什么叫泰森多边形?)

泰森多边形的画法步骤：

1、首先打开arccatlog，将文件关联到我们需要处理的文件夹。然后添加数据里面找到我们需要添加的数据进行添加

2、在连接的文件夹下新建个人地理数据库，并创建要素数据集，选择墨卡托坐标系，和WGS84坐标系

3、在要素集下新建点要素，并新建线要素泰森分界线

4、打开编辑器，在编辑窗口里面找到创建要素，并用点构造工具进行构造站

5、根据系统工具——分析工具——领域分析——创建泰森多边形，输入要素选择构造的站

6、选择开始编辑，用线构造工具，根据泰勒多边形勾勒出泰森边界的轮廓

7、去掉泰森多边形图层前面的勾，然后修改雨量站和泰森边界的符号系统，就绘制出了泰森多边形

泰森多边形的特性：

1、每个泰森多边形内仅含有一个离散点数据；

2、泰森多边形内的点到相应离散点的距离最近；

3、位于泰森多边形边上的点到其两边的离散点的距离相等。

泰森多边形可用于定性分析、统计分析、邻近分析等。例如，可以用离散点的性质来描述泰森多边形区域的性质；可用离散点的数据来计算泰森多边形区域的数据；当某一数据点落入某一泰森多边形中时，它与相应的离散点最邻近，无需计算距离。

在泰森多边形的构建中，首先要将离散点构成三角网。这种三角网称为Delaunay三角网。（来自百度）

一：泰森多边形是什么 说简单点、什么叫泰森多边形?

二：求c++的 泰森多边形、什么叫泰森多边形?

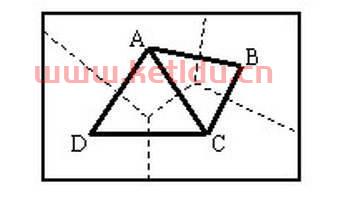
提起泰森多边形，学过水文的恐怕没有一个不熟悉，“它是求解流域面平均降雨量的一大法宝”，上大学时，我的老师这样告诉我。后来我也就一直持有这样的信念，从不怀疑，也从未思索。直到上周，我去研究生院给2007年级研究生讲《水土保持学原理》的有关水文的内容，在我也津津乐道地讲授了这个法宝后，一个的学生的提问震撼了这片原本风平浪静的世界。在描述学生的提问之前，首先让我们来回顾一下泰森多边形。泰森多边形的始祖要追溯到1908年，G.Voronoi首先在数学上限定了每个离散点数据的有效作用范围，即其有效反映区域信息的范围，并定义了二维平面上的Voronoi图(Voronoi， 1908）。1911年，荷兰气候学家A.H.Thiessen应用Voronoi图进行了大区域内的平均降水量研究(Thiessen, 1911)。1934年，B.Delaunay由Voronoi图演化出了更易于分析应用的Delaunay三角网（Delaunary, 1934, 武晓波等， 1999）。本来那个图，那个多变形，原本有很多名字，有叫Voronoi图的，有叫Delaunay三角网，还有人叫Dirichlet多边形图(是否就是藉工给大家介绍的大数学家(籍利平，2007），我还没查证到，先打住)， 但大多数水文人则只记住了泰森多边形的名字。泰森多边形法是一种根据离散分布的气象站的降雨量来计算平均降雨量的方法。具体做法是，将所有相邻气象站连成三角形，作这些三角形各边的垂直平分线，于是每个气象站周围的若干垂直平分线便围成一个多边形。可用这个多边形内所包含的一个*气象站的降雨强度来表示这个多边形区域内的降雨强度，并称这个多边形为泰森多边形。下图是我给学生讲课时采用的图。（博主（2008feb11）注: 此图阴影部分绘错，正确的图见博文http://www.sciencenet.cn/blog/user_content.aspx?id=15628 中的图2，谢谢小河海纠错） 我讲课时，认为，站点B对流域的贡献面积是多边形BefgB。课间休息，一个女学生喊住我，说，站点B对流域的贡献面积应该是阴影所示的面积，她学校的老师是这样告诉她的。经她这样一提，我马上领会到，即使我本次课所讲全部正确，那么这一点真真切切是我讲错了。事实上，在备课时，我隐隐约约思考过这个问题。我备课时的思考逻辑是，既然是泰森多边形法，必须有多边形在里边。既然是多边形，必须是直边组成的图形吧(见下面参考文献列出的多边形的定义），那么泰森多边形就非BefgB多边形莫属了。坦白地说，从学校毕业出来，从来没有亲自用泰森多边形法计算过流域面平均雨量。初步估算一般均是采用等权重的算术平均法，而精确的模拟则往往直接交付给计算机，因为现成的程序比比皆是(张德伟等，1991）。于是，“想当然”就这样大模大样地出现在学生面前，对此我非常抱歉。如果我没记错，泰森多边形始出于计算规则区域的空间面平均降雨量，因之诞生了许许多多的多边形，所以叫泰森多边形。但对于流域，由于流域的边界一般是曲线，所以严格地说，对于流域而言，泰森多边形（即上面图形中的阴影）不能称之为泰森多边形，而应该称之为泰森曲边形。相应地，对水文人来讲，泰森多边形法是否可以改名为泰森曲边形法 如果Yes，那将会消除多少误解啊，起码对我这样的人来讲。也许我这句话音未落，马上会迎来专家拍砖。如果那样，真是感激不尽，君不知，此时的我是多么盼望高手指点，为我前面的错找到一点点“对”的理由。再次感谢该班可爱的学生。没有他们，我可能一直没有机会思考这个问题。参考文献：1. Voronoi G. Nouvelles Applications des Parameters Continus, a la Theorie des Formes Quadratiques, Deuxieme Memorie: Recherches sur les Parrallelloedres Primitifs, Jounal fur die Reine und Angewandte Mathematik, 1908(134)： 198～2872. Thiessen A H. Precipitation Averages for Large Areas, Monthly Weather Review, 1911(39):1082～10843. Delaunay B. Sur la Sphere Vide. Bulletin of the Academy of Sciences of the USSR, Classe des Sciences Mathematiques et Naturelles, 1934(8):793～8004. 武晓波，王世新，肖春生，Delaunay三角网的生成算法研究， 测绘学报，1999， 28（2）5. 籍利平，2007-8-17， “Dirichlet开始了柏林数学的黄金时代” 科学网(http://www.kexue.com.cn/blog/user_content.aspx?id=6110) 。6. polygon的定义是A closed plane figure bounded by three or more line segments，或者 a closed plane figure bounded by straight sides（http://www.thefreedictionary.com/polygon），多边形的定义是:给出一系列共面的点A1,A2,...,An,将这些点依次用线段连接,最后,An与A1相连.这样,A1,A2,...,An是多边形的顶点,连接顶点间的线段称为边(软件学报) 2000年 王文成,吴恩华）7. 张德伟，崔永生，在计算机上应用泰森多边形法计算流域面平均雨量，水文， 1991， (1)。

免责声明
           本站所有信息均来自互联网搜集
1.与产品相关信息的真实性准确性均由发布单位及个人负责，
2.拒绝任何人以任何形式在本站发表与中华人民共和国法律相抵触的言论
3.请大家仔细辨认！并不代表本站观点,本站对此不承担任何相关法律责任！
4.如果发现本网站有任何文章侵犯你的权益,请立刻联系本站站长[QQ:775191930]，通知给予删除